Graph

Table of Contents

• 200. Number of Islands (Medium)
• 130. Surrounded Regions (Medium)
• 133. Clone Graph (Medium)
• 399. Evaluate Division (Medium)
• 207. Course Schedule (Medium)
• 210. Course Schedule II (Medium)

200. Number of Islands

• LeetCode | LeetCode CH (Medium)

• Tags: array, depth first search, breadth first search, union find, matrix

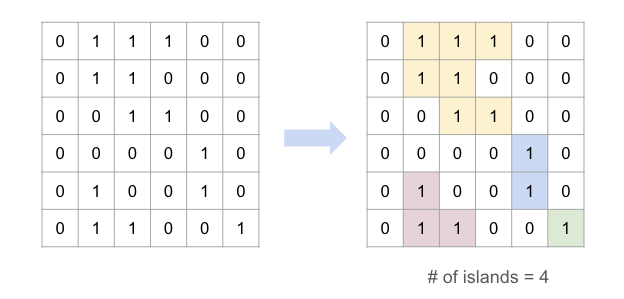
• Count the number of islands in a 2D grid.
• Method 1: DFS

• Method 2: BFS (use a queue to traverse the grid)

• How to keep track of visited cells?

  1. Mark the visited cell as 0 (or any other value) to avoid revisiting it.
  2. Use a set to store the visited cells.

• Steps:

  1. Init: variables
  2. DFS/BFS: starting from the cell with 1, turn all the connected 1s to 0.
  3. Traverse the grid, and if the cell is 1, increment the count and call DFS/BFS.

200. Number of Islands - Python Solution

from collections import deque
from copy import deepcopy
from typing import List


# DFS
def numIslandsDFS(grid: List[List[str]]) -> int:
    if not grid:
        return 0

    m, n = len(grid), len(grid[0])
    res = 0

    def dfs(r, c):
        if r < 0 or r >= m or c < 0 or c >= n or grid[r][c] != "1":
            return

        grid[r][c] = "2"

        dfs(r + 1, c)
        dfs(r - 1, c)
        dfs(r, c + 1)
        dfs(r, c - 1)

    for r in range(m):
        for c in range(n):
            if grid[r][c] == "1":
                dfs(r, c)
                res += 1

    return res


# BFS + Set
def numIslandsBFS1(grid: List[List[str]]) -> int:
    if not grid:
        return 0

    m, n = len(grid), len(grid[0])
    dirs = [(1, 0), (-1, 0), (0, 1), (0, -1)]
    visited = set()
    res = 0

    def bfs(r, c):
        q = deque([(r, c)])

        while q:
            row, col = q.popleft()

            for dr, dc in dirs:
                nr, nc = row + dr, col + dc
                if (
                    nr < 0
                    or nr >= m
                    or nc < 0
                    or nc >= n
                    or grid[nr][nc] == "0"
                    or (nr, nc) in visited
                ):
                    continue

                visited.add((nr, nc))
                q.append((nr, nc))

    for r in range(m):
        for c in range(n):
            if grid[r][c] == "1" and (r, c) not in visited:
                visited.add((r, c))
                bfs(r, c)
                res += 1

    return res


# BFS + Grid
def numIslandsBFS2(grid: List[List[str]]) -> int:
    if not grid:
        return 0

    m, n = len(grid), len(grid[0])
    dirs = [[0, 1], [0, -1], [1, 0], [-1, 0]]
    res = 0

    def bfs(r, c):
        q = deque([(r, c)])

        while q:
            row, col = q.popleft()

            for dr, dc in dirs:
                nr, nc = dr + row, dc + col
                if (
                    nr < 0
                    or nr >= m
                    or nc < 0
                    or nc >= n
                    or grid[nr][nc] != "1"
                ):
                    continue
                grid[nr][nc] = "2"
                q.append((nr, nc))

    for i in range(m):
        for j in range(n):
            if grid[i][j] == "1":
                grid[i][j] = "2"
                bfs(i, j)
                res += 1

    return res


grid = [
    ["1", "1", "1", "1", "0"],
    ["1", "1", "0", "1", "0"],
    ["1", "1", "0", "0", "0"],
    ["0", "0", "0", "0", "0"],
]

print(numIslandsDFS(deepcopy(grid)))  # 1
print(numIslandsBFS1(deepcopy(grid)))  # 1
print(numIslandsBFS2(deepcopy(grid)))  # 1

200. Number of Islands - C++ Solution

#include <vector>
#include <iostream>
using namespace std;

class Solution
{
private:
    void dfs(vector<vector<char>> &grid, int r, int c)
    {
        int row = grid.size();
        int col = grid[0].size();

        if (r < 0 || r >= row || c < 0 || c >= col || grid[r][c] != '1')
        {
            return;
        }
        grid[r][c] = '0';

        dfs(grid, r - 1, c);
        dfs(grid, r + 1, c);
        dfs(grid, r, c - 1);
        dfs(grid, r, c + 1);
    }

public:
    int numIslands(vector<vector<char>> &grid)
    {
        int m = grid.size(), n = grid[0].size();
        int res = 0;
        for (int i = 0; i < m; i++)
        {
            for (int j = 0; j < n; j++)
            {
                if (grid[i][j] == '1')
                {
                    res++;
                    dfs(grid, i, j);
                }
            }
        }
        return res;
    }
};

int main()
{
    Solution s;
    vector<vector<char>> grid = {
        {'1', '1', '0', '0', '0'},
        {'1', '1', '0', '0', '0'},
        {'0', '0', '1', '0', '0'},
        {'0', '0', '0', '1', '1'}};
    cout << s.numIslands(grid) << endl;
    return 0;
}

130. Surrounded Regions

• LeetCode | LeetCode CH (Medium)

• Tags: array, depth first search, breadth first search, union find, matrix

130. Surrounded Regions - Python Solution

from collections import deque
from copy import deepcopy
from pprint import pprint
from typing import List


# 1. DFS
def solveDFS(board: List[List[str]]) -> None:
    """
    Do not return anything, modify board in-place instead.
    """
    if not board and not board[0]:
        return None

    m, n = len(board), len(board[0])

    def capture(r, c):
        if r not in range(m) or c not in range(n) or board[r][c] != "O":
            return None

        board[r][c] = "T"
        capture(r + 1, c)
        capture(r - 1, c)
        capture(r, c + 1)
        capture(r, c - 1)

    for r in range(m):
        for c in range(n):
            if board[r][c] == "O" and (r in [0, m - 1] or c in [0, n - 1]):
                capture(r, c)

    for r in range(m):
        for c in range(n):
            if board[r][c] == "O":
                board[r][c] = "X"

    for r in range(m):
        for c in range(n):
            if board[r][c] == "T":
                board[r][c] = "O"


# 2. BFS
def solveBFS(board: List[List[str]]) -> None:
    """
    Do not return anything, modify board in-place instead.
    """
    if not board and not board[0]:
        return None

    m, n = len(board), len(board[0])
    directions = [(1, 0), (-1, 0), (0, 1), (0, -1)]

    def capture(r, c):
        q = deque([(r, c)])

        while q:
            row, col = q.popleft()

            for dr, dc in directions:
                nr = row + dr
                nc = col + dc
                if nr in range(m) and nc in range(n) and board[nr][nc] == "O":
                    q.append((nr, nc))
                    board[nr][nc] = "T"

    for r in range(m):
        for c in range(n):
            if board[r][c] == "O" and (r in [0, m - 1] or c in [0, n - 1]):
                board[r][c] = "T"
                capture(r, c)

    for r in range(m):
        for c in range(n):
            if board[r][c] == "O":
                board[r][c] = "X"

    for r in range(m):
        for c in range(n):
            if board[r][c] == "T":
                board[r][c] = "O"


board = [
    ["X", "X", "X", "X"],
    ["X", "O", "O", "X"],
    ["X", "X", "O", "X"],
    ["X", "O", "X", "X"],
]
board1 = deepcopy(board)
solveDFS(board1)
pprint(board1)
# [['X', 'X', 'X', 'X'],
#  ['X', 'X', 'X', 'X'],
#  ['X', 'X', 'X', 'X'],
#  ['X', 'O', 'X', 'X']]

board2 = deepcopy(board)
solveBFS(board2)
pprint(board2)
# [['X', 'X', 'X', 'X'],
#  ['X', 'X', 'X', 'X'],
#  ['X', 'X', 'X', 'X'],
#  ['X', 'O', 'X', 'X']]

133. Clone Graph

• LeetCode | LeetCode CH (Medium)

• Tags: hash table, depth first search, breadth first search, graph

133. Clone Graph - Python Solution

from collections import deque
from typing import Optional


class Node:
    def __init__(self, val=0, neighbors=None):
        self.val = val
        self.neighbors = neighbors if neighbors is not None else []


# 1. DFS
def cloneGraphDFS(node: Optional["Node"]) -> Optional["Node"]:
    if not node:
        return None

    cloned = {}  # {old: new}

    def dfs(node):
        if node in cloned:
            return cloned[node]

        new = Node(node.val)
        cloned[node] = new

        for neighbor in node.neighbors:
            new.neighbors.append(dfs(neighbor))

        return new

    return dfs(node)


# 2. BFS
def cloneGraphBFS(node: Optional["Node"]) -> Optional["Node"]:
    if not node:
        return None

    cloned = {node: Node(node.val)}
    q = deque([node])

    while q:
        cur = q.popleft()

        for neighbor in cur.neighbors:
            if neighbor not in cloned:
                cloned[neighbor] = Node(neighbor.val)
                q.append(neighbor)

            cloned[cur].neighbors.append(cloned[neighbor])

    return cloned[node]

399. Evaluate Division

• LeetCode | LeetCode CH (Medium)

• Tags: array, string, depth first search, breadth first search, union find, graph, shortest path

399. Evaluate Division - Python Solution

from collections import defaultdict
from typing import List


# Union Find
def calcEquation(
    equations: List[List[str]], values: List[float], queries: List[List[str]]
) -> List[float]:
    graph = defaultdict(dict)
    for (a, b), v in zip(equations, values):
        graph[a][b] = v
        graph[b][a] = 1 / v

    def dfs(a, b, visited):
        if a not in graph or b not in graph:
            return -1.0

        if b in graph[a]:
            return graph[a][b]

        for c in graph[a]:
            if c not in visited:
                visited.add(c)
                d = dfs(c, b, visited)
                if d != -1.0:
                    return graph[a][c] * d
        return -1.0

    result = []
    for a, b in queries:
        result.append(dfs(a, b, set()))

    return result


equations = [["a", "b"], ["b", "c"]]
values = [2.0, 3.0]
queries = [["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"]]
print(calcEquation(equations, values, queries))  # [6.0, 0.5, -1.0, 1.0, -1.0]

207. Course Schedule

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

• Return true if it is possible to finish all courses, otherwise return false.
• Dependency relationships imply the topological sort algorithm.
• Cycle detection
• Topological Sort
• DAG (Directed Acyclic Graph)
• Time complexity: O(V+E)
• Space complexity: O(V+E)
• Prerequisites: Indegree (Look at the problem 1557. Minimum Number of Vertices to Reach All Nodes)
  • Indegree: Number of incoming edges to a vertex
• Applications: task scheduling, course scheduling, build systems, dependency resolution, compiler optimization, etc.

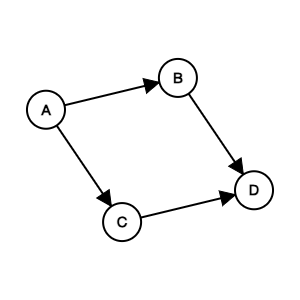
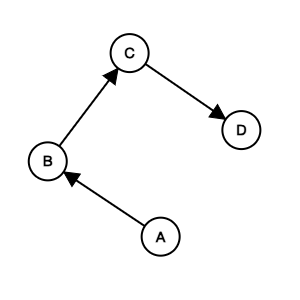
Course to prerequisites mapping

flowchart LR
    0((0)) --> 1((1))
    0((0)) --> 2((2))
    1((1)) --> 3((3))
    3((3)) --> 4((4))
    1((1)) --> 4((4))

Prerequisites to course mapping

flowchart LR
    1((1)) --> 0((0))
    2((2)) --> 0((0))
    3((3)) --> 1((1))
    4((4)) --> 3((3))
    4((4)) --> 1((1))

course	0	0	1	1	3
prerequisite	1	2	3	4	4

index	0	1	2	3	4
in-degree	0	0	0	0	0

Initialize

• graph

prerequisite	1	2	3	4
course	[0]	[0]	[1]	[1, 3]

• in-degree

	0	1	2	3	4
in-degree	2	2	0	1	0

• queue: [2, 4]
• pop 2 from the queue

flowchart LR
    1((1)) --> 0((0))
    3((3)) --> 1((1))
    4((4)) --> 3((3))
    4((4)) --> 1((1))

	0	1	2	3	4
in-degree	1	2	0	1	0

• queue: [4]
• pop 4 from the queue

flowchart LR
    1((1)) --> 0((0))
    3((3)) --> 1((1))

	0	1	2	3	4
in-degree	1	1	0	0	0

• queue: [3]
• pop 3 from the queue

flowchart LR
    1((1)) --> 0((0))

	0	1	2	3	4
in-degree	1	0	0	0	0

• queue: [1]
• pop 1 from the queue

flowchart LR
    0((0))

	0	1	2	3	4
in-degree	0	0	0	0	0

• queue: [0]
• pop 0 from the queue
• All courses are taken. Return True.

207. Course Schedule - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS (Kahn's Algorithm)
def canFinishBFS(numCourses: int, prerequisites: List[List[int]]) -> bool:
    graph = defaultdict(list)
    indegree = defaultdict(int)

    for crs, pre in prerequisites:
        graph[pre].append(crs)
        indegree[crs] += 1

    q = deque([i for i in range(numCourses) if indegree[i] == 0])
    count = 0

    while q:
        crs = q.popleft()
        count += 1

        for nxt in graph[crs]:
            indegree[nxt] -= 1

            if indegree[nxt] == 0:
                q.append(nxt)

    return count == numCourses


# DFS + Set
def canFinishDFS1(numCourses: int, prerequisites: List[List[int]]) -> bool:
    graph = defaultdict(list)
    for crs, pre in prerequisites:
        graph[crs].append(pre)

    visiting = set()

    def dfs(crs):
        if crs in visiting:  # cycle detected
            return False
        if graph[crs] == []:
            return True

        visiting.add(crs)

        for pre in graph[crs]:
            if not dfs(pre):
                return False

        visiting.remove(crs)
        graph[crs] = []

        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return False
    return True


# DFS + List
def canFinishDFS2(numCourses: int, prerequisites: List[List[int]]) -> bool:
    graph = defaultdict(list)
    for pre, crs in prerequisites:
        graph[crs].append(pre)

    # 0: init, 1: visiting, 2: visited
    status = [0] * numCourses

    def dfs(crs):
        if status[crs] == 1:  # cycle detected
            return False
        if status[crs] == 2:
            return True

        status[crs] = 1

        for pre in graph[crs]:
            if not dfs(pre):
                return False

        status[crs] = 2
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return False
    return True


prerequisites = [[0, 1], [0, 2], [1, 3], [1, 4], [3, 4]]
print(canFinishBFS(5, prerequisites))  # True
print(canFinishDFS1(5, prerequisites))  # True
print(canFinishDFS2(5, prerequisites))  # True

207. Course Schedule - C++ Solution

#include <functional>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;

class Solution {
   public:
    // BFS
    bool canFinishBFS(int numCourses, vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> indegree(numCourses, 0);
        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
            indegree[pre[0]]++;
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        int cnt = 0;
        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            cnt++;

            for (int nxt : graph[cur]) {
                indegree[nxt]--;
                if (indegree[nxt] == 0) {
                    q.push(nxt);
                }
            }
        }
        return cnt == numCourses;
    }

    // DFS
    bool canFinishDFS(int numCourses, vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
        }
        // 0: not visited, 1: visiting, 2: visited
        vector<int> state(numCourses, 0);

        function<bool(int)> dfs = [&](int pre) -> bool {
            state[pre] = 1;  // visiting
            for (int crs : graph[pre]) {
                if (state[crs] == 1 || (state[crs] == 0 && dfs(crs))) {
                    return true;
                }
            }
            state[pre] = 2;  // visited
            return false;
        };

        for (int i = 0; i < numCourses; i++) {
            if (state[i] == 0 && dfs(i)) {
                return false;
            }
        }
        return true;
    }
};

int main() {
    Solution sol;
    vector<vector<int>> prerequisites = {{1, 0}, {2, 1}, {3, 2}, {4, 3},
                                         {5, 4}, {6, 5}, {7, 6}, {8, 7},
                                         {9, 8}, {10, 9}};
    int numCourses = 11;
    cout << sol.canFinishBFS(numCourses, prerequisites) << endl;
    cout << sol.canFinishDFS(numCourses, prerequisites) << endl;
    return 0;
}

210. Course Schedule II

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

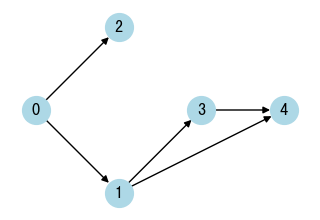
• Return the ordering of courses you should take to finish all courses. If there are multiple valid answers, return any of them.

210. Course Schedule II - Python Solution

from collections import defaultdict, deque
from typing import List


# 1. BFS - Kahn's Algorithm
def findOrderBFS(numCourses: int, prerequisites: List[List[int]]) -> List[int]:
    graph = defaultdict(list)
    indegree = defaultdict(int)

    for crs, pre in prerequisites:
        graph[pre].append(crs)
        indegree[crs] += 1

    q = deque([i for i in range(numCourses) if indegree[i] == 0])
    order = []

    while q:
        pre = q.popleft()
        order.append(pre)

        for crs in graph[pre]:
            indegree[crs] -= 1
            if indegree[crs] == 0:
                q.append(crs)

    return order if len(order) == numCourses else []


# 2. DFS + Set
def findOrderDFS1(
    numCourses: int, prerequisites: List[List[int]]
) -> List[int]:
    adj = defaultdict(list)
    for crs, pre in prerequisites:
        adj[crs].append(pre)

    visit, cycle = set(), set()
    order = []

    def dfs(crs):
        if crs in cycle:
            return False
        if crs in visit:
            return True

        cycle.add(crs)
        for pre in adj[crs]:
            if not dfs(pre):
                return False

        cycle.remove(crs)
        visit.add(crs)
        order.append(crs)
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return []

    return order


# 3. DFS + List
def findOrderDFS2(
    numCourses: int, prerequisites: List[List[int]]
) -> List[int]:
    adj = defaultdict(list)
    for pre, crs in prerequisites:
        adj[crs].append(pre)

    # 0: not visited, 1: visiting, 2: visited
    state = [0] * numCourses
    order = []

    def dfs(crs):
        if state[crs] == 1:
            return False
        if state[crs] == 2:
            return True

        state[crs] = 1

        for pre in adj[crs]:
            if not dfs(pre):
                return False

        state[crs] = 2
        order.append(crs)
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return []

    return order[::-1]


numCourses = 5
prerequisites = [[0, 1], [0, 2], [1, 3], [1, 4], [3, 4]]
print(findOrderBFS(numCourses, prerequisites))  # [2, 4, 3, 1, 0]
print(findOrderDFS1(numCourses, prerequisites))  # [4, 3, 1, 2, 0]
print(findOrderDFS2(numCourses, prerequisites))  # [4, 3, 2, 1, 0]

210. Course Schedule II - C++ Solution

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

class Solution {
   public:
    // BFS
    vector<int> findOrderBFS(int numCourses,
                             vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> indegree(numCourses, 0);

        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
            indegree[pre[0]]++;
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++)
            if (indegree[i] == 0) q.push(i);

        vector<int> order;

        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            order.push_back(cur);

            for (int nxt : graph[cur]) {
                indegree[nxt]--;
                if (indegree[nxt] == 0) q.push(nxt);
            }
        }

        return (int)order.size() == numCourses ? order : vector<int>{};
    }
};

int main() {
    Solution obj;
    vector<vector<int>> prerequisites{{1, 0}, {2, 0}, {3, 1}, {3, 2}};
    vector<int> res = obj.findOrderBFS(4, prerequisites);
    for (size_t i = 0; i < res.size(); i++) cout << res[i] << "\n";
    return 0;
}

Comments