Topological Sort¶

Table of Contents¶

207. Course Schedule (Medium)
210. Course Schedule II (Medium)
269. Alien Dictionary (Hard) 👑
1203. Sort Items by Groups Respecting Dependencies (Hard)
1857. Largest Color Value in a Directed Graph (Hard)

207. Course Schedule¶

LeetCode | LeetCode CH (Medium)
Tags: depth first search, breadth first search, graph, topological sort
Return true if it is possible to finish all courses, otherwise return false.
Dependency relationships imply the topological sort algorithm.
Cycle detection
Topological Sort
DAG (Directed Acyclic Graph)
Time complexity: O(V+E)
Space complexity: O(V+E)
Prerequisites: Indegree (Look at the problem 1557. Minimum Number of Vertices to Reach All Nodes)
- Indegree: Number of incoming edges to a vertex
Applications: task scheduling, course scheduling, build systems, dependency resolution, compiler optimization, etc.

ts1

ts2

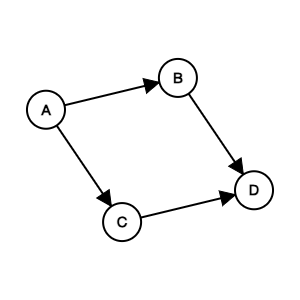
Course to prerequisites mapping

flowchart LR
    0((0)) --> 1((1))
    0((0)) --> 2((2))
    1((1)) --> 3((3))
    3((3)) --> 4((4))
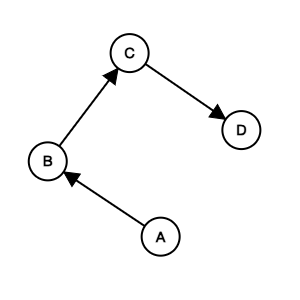
    1((1)) --> 4((4))

Prerequisites to course mapping

flowchart LR
    1((1)) --> 0((0))
    2((2)) --> 0((0))
    3((3)) --> 1((1))
    4((4)) --> 3((3))
    4((4)) --> 1((1))

course	0	0	1	1	3
prerequisite	1	2	3	4	4

index	0	1	2	3	4
in-degree	0	0	0	0	0

Initialize

graph

prerequisite	1	2	3	4
course	`[0]`	`[0]`	`[1]`	`[1, 3]`

in-degree

	0	1	2	3	4
in-degree	2	2	0	1	0

queue: [2, 4]
pop 2 from the queue

flowchart LR
    1((1)) --> 0((0))
    3((3)) --> 1((1))
    4((4)) --> 3((3))
    4((4)) --> 1((1))

	0	1	2	3	4
in-degree	1	2	0	1	0

queue: [4]
pop 4 from the queue

flowchart LR
    1((1)) --> 0((0))
    3((3)) --> 1((1))

	0	1	2	3	4
in-degree	1	1	0	0	0

queue: [3]
pop 3 from the queue

flowchart LR
    1((1)) --> 0((0))

	0	1	2	3	4
in-degree	1	0	0	0	0

queue: [1]
pop 1 from the queue

flowchart LR
    0((0))

	0	1	2	3	4
in-degree	0	0	0	0	0

queue: [0]
pop 0 from the queue
All courses are taken. Return True.

207. Course Schedule - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS (Kahn's Algorithm)
def canFinishBFS(numCourses: int, prerequisites: List[List[int]]) -> bool:
    graph = defaultdict(list)
    indegree = defaultdict(int)

    for crs, pre in prerequisites:
        graph[pre].append(crs)
        indegree[crs] += 1

    q = deque([i for i in range(numCourses) if indegree[i] == 0])
    count = 0

    while q:
        crs = q.popleft()
        count += 1

        for nxt in graph[crs]:
            indegree[nxt] -= 1

            if indegree[nxt] == 0:
                q.append(nxt)

    return count == numCourses


# DFS + Set
def canFinishDFS1(numCourses: int, prerequisites: List[List[int]]) -> bool:
    graph = defaultdict(list)
    for crs, pre in prerequisites:
        graph[crs].append(pre)

    visiting = set()

    def dfs(crs):
        if crs in visiting:  # cycle detected
            return False
        if graph[crs] == []:
            return True

        visiting.add(crs)

        for pre in graph[crs]:
            if not dfs(pre):
                return False

        visiting.remove(crs)
        graph[crs] = []

        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return False
    return True


# DFS + List
def canFinishDFS2(numCourses: int, prerequisites: List[List[int]]) -> bool:
    graph = defaultdict(list)
    for pre, crs in prerequisites:
        graph[crs].append(pre)

    # 0: init, 1: visiting, 2: visited
    status = [0] * numCourses

    def dfs(crs):
        if status[crs] == 1:  # cycle detected
            return False
        if status[crs] == 2:
            return True

        status[crs] = 1

        for pre in graph[crs]:
            if not dfs(pre):
                return False

        status[crs] = 2
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return False
    return True


prerequisites = [[0, 1], [0, 2], [1, 3], [1, 4], [3, 4]]
print(canFinishBFS(5, prerequisites))  # True
print(canFinishDFS1(5, prerequisites))  # True
print(canFinishDFS2(5, prerequisites))  # True

207. Course Schedule - C++ Solution

#include <functional>
#include <iostream>
#include <queue>
#include <vector>
using namespace std;

class Solution {
   public:
    // BFS
    bool canFinishBFS(int numCourses, vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> indegree(numCourses, 0);
        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
            indegree[pre[0]]++;
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++) {
            if (indegree[i] == 0) {
                q.push(i);
            }
        }

        int cnt = 0;
        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            cnt++;

            for (int nxt : graph[cur]) {
                indegree[nxt]--;
                if (indegree[nxt] == 0) {
                    q.push(nxt);
                }
            }
        }
        return cnt == numCourses;
    }

    // DFS
    bool canFinishDFS(int numCourses, vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
        }
        // 0: not visited, 1: visiting, 2: visited
        vector<int> state(numCourses, 0);

        function<bool(int)> dfs = [&](int pre) -> bool {
            state[pre] = 1;  // visiting
            for (int crs : graph[pre]) {
                if (state[crs] == 1 || (state[crs] == 0 && dfs(crs))) {
                    return true;
                }
            }
            state[pre] = 2;  // visited
            return false;
        };

        for (int i = 0; i < numCourses; i++) {
            if (state[i] == 0 && dfs(i)) {
                return false;
            }
        }
        return true;
    }
};

int main() {
    Solution sol;
    vector<vector<int>> prerequisites = {{1, 0}, {2, 1}, {3, 2}, {4, 3},
                                         {5, 4}, {6, 5}, {7, 6}, {8, 7},
                                         {9, 8}, {10, 9}};
    int numCourses = 11;
    cout << sol.canFinishBFS(numCourses, prerequisites) << endl;
    cout << sol.canFinishDFS(numCourses, prerequisites) << endl;
    return 0;
}

210. Course Schedule II¶

LeetCode | LeetCode CH (Medium)
Tags: depth first search, breadth first search, graph, topological sort
Return the ordering of courses you should take to finish all courses. If there are multiple valid answers, return any of them.

0207

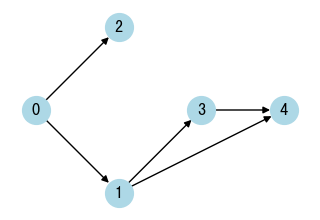
210. Course Schedule II - Python Solution

from collections import defaultdict, deque
from typing import List


# 1. BFS - Kahn's Algorithm
def findOrderBFS(numCourses: int, prerequisites: List[List[int]]) -> List[int]:
    graph = defaultdict(list)
    indegree = defaultdict(int)

    for crs, pre in prerequisites:
        graph[pre].append(crs)
        indegree[crs] += 1

    q = deque([i for i in range(numCourses) if indegree[i] == 0])
    order = []

    while q:
        pre = q.popleft()
        order.append(pre)

        for crs in graph[pre]:
            indegree[crs] -= 1
            if indegree[crs] == 0:
                q.append(crs)

    return order if len(order) == numCourses else []


# 2. DFS + Set
def findOrderDFS1(
    numCourses: int, prerequisites: List[List[int]]
) -> List[int]:
    adj = defaultdict(list)
    for crs, pre in prerequisites:
        adj[crs].append(pre)

    visit, cycle = set(), set()
    order = []

    def dfs(crs):
        if crs in cycle:
            return False
        if crs in visit:
            return True

        cycle.add(crs)
        for pre in adj[crs]:
            if not dfs(pre):
                return False

        cycle.remove(crs)
        visit.add(crs)
        order.append(crs)
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return []

    return order


# 3. DFS + List
def findOrderDFS2(
    numCourses: int, prerequisites: List[List[int]]
) -> List[int]:
    adj = defaultdict(list)
    for pre, crs in prerequisites:
        adj[crs].append(pre)

    # 0: not visited, 1: visiting, 2: visited
    state = [0] * numCourses
    order = []

    def dfs(crs):
        if state[crs] == 1:
            return False
        if state[crs] == 2:
            return True

        state[crs] = 1

        for pre in adj[crs]:
            if not dfs(pre):
                return False

        state[crs] = 2
        order.append(crs)
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return []

    return order[::-1]


numCourses = 5
prerequisites = [[0, 1], [0, 2], [1, 3], [1, 4], [3, 4]]
print(findOrderBFS(numCourses, prerequisites))  # [2, 4, 3, 1, 0]
print(findOrderDFS1(numCourses, prerequisites))  # [4, 3, 1, 2, 0]
print(findOrderDFS2(numCourses, prerequisites))  # [4, 3, 2, 1, 0]

210. Course Schedule II - C++ Solution

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

class Solution {
   public:
    // BFS
    vector<int> findOrderBFS(int numCourses,
                             vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> indegree(numCourses, 0);

        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
            indegree[pre[0]]++;
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++)
            if (indegree[i] == 0) q.push(i);

        vector<int> order;

        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            order.push_back(cur);

            for (int nxt : graph[cur]) {
                indegree[nxt]--;
                if (indegree[nxt] == 0) q.push(nxt);
            }
        }

        return (int)order.size() == numCourses ? order : vector<int>{};
    }
};

int main() {
    Solution obj;
    vector<vector<int>> prerequisites{{1, 0}, {2, 0}, {3, 1}, {3, 2}};
    vector<int> res = obj.findOrderBFS(4, prerequisites);
    for (size_t i = 0; i < res.size(); i++) cout << res[i] << "\n";
    return 0;
}

269. Alien Dictionary¶

LeetCode | LeetCode CH (Hard)
Tags: array, string, depth first search, breadth first search, graph, topological sort
Return the correct order of characters in the alien language.

269. Alien Dictionary - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS - Kahn's algorithm (Topological Sort)
def alienOrderBFS(words: List[str]) -> str:
    graph = defaultdict(set)
    indegree = {c: 0 for word in words for c in word}

    for i in range(len(words) - 1):
        w1, w2 = words[i], words[i + 1]
        minLen = min(len(w1), len(w2))

        if len(w1) > len(w2) and w1[:minLen] == w2[:minLen]:
            return ""

        for j in range(minLen):
            if w1[j] != w2[j]:
                if w2[j] not in graph[w1[j]]:
                    graph[w1[j]].add(w2[j])
                    indegree[w2[j]] += 1
                break

    q = deque([c for c in indegree if indegree[c] == 0])
    result = []

    while q:
        char = q.popleft()
        result.append(char)

        for neighbor in graph[char]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                q.append(neighbor)

    return "".join(result) if len(result) == len(indegree) else ""


# DFS - Topological Sort
def alienOrderDFS(words: List[str]) -> str:
    graph = defaultdict(set)
    visited = {}
    result = []

    for i in range(len(words) - 1):
        w1, w2 = words[i], words[i + 1]
        minLen = min(len(w1), len(w2))

        if len(w1) > len(w2) and w1[:minLen] == w2[:minLen]:
            return ""

        for j in range(minLen):
            if w1[j] != w2[j]:
                if w2[j] not in graph[w1[j]]:
                    graph[w1[j]].add(w2[j])
                break

    def dfs(c):
        if c in visited:
            return visited[c]

        visited[c] = False
        for neighbor in graph[c]:
            if not dfs(neighbor):
                return False

        visited[c] = True
        result.append(c)
        return True

    for c in list(graph.keys()):
        if not dfs(c):
            return ""

    return "".join(result[::-1])


words = ["wrt", "wrf", "er", "ett", "rftt"]
print(alienOrderBFS(words))  # wertf
print(alienOrderDFS(words))  # wertf

1203. Sort Items by Groups Respecting Dependencies¶

LeetCode | LeetCode CH (Hard)
Tags: depth first search, breadth first search, graph, topological sort
Return any permutation of the items that satisfies the requirements.

1203. Sort Items by Groups Respecting Dependencies - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS - Kahn's algorithm (Topological Sort)
def sortItems(
    n: int, m: int, group: List[int], beforeItems: List[List[int]]
) -> List[int]:
    def topological_sort(graph, indegree, nodes):
        q = deque([node for node in nodes if indegree[node] == 0])
        result = []

        while q:
            node = q.popleft()
            result.append(node)

            for neighbor in graph[node]:
                indegree[neighbor] -= 1
                if indegree[neighbor] == 0:
                    q.append(neighbor)

        return result if len(result) == len(nodes) else []

    groupItems = defaultdict(list)
    groupGraph = defaultdict(set)
    groupIndegree = defaultdict(int)
    itemGraph = defaultdict(set)
    itemIndegree = defaultdict(int)

    for i in range(n):
        if group[i] == -1:
            group[i] = m
            m += 1
        groupItems[group[i]].append(i)

    for i, beforeItem in enumerate(beforeItems):
        for before in beforeItem:
            if group[before] != group[i]:
                if group[i] not in groupGraph[group[before]]:
                    groupGraph[group[before]].add(group[i])
                    groupIndegree[group[i]] += 1
            else:
                itemGraph[before].add(i)
                itemIndegree[i] += 1

    allGroups = list(set(group))
    groupOrder = topological_sort(groupGraph, groupIndegree, allGroups)
    if not groupOrder:
        return []

    result = []
    for g in groupOrder:
        items = groupItems[g]
        itemOrder = topological_sort(itemGraph, itemIndegree, items)
        if not itemOrder:
            return []
        result.extend(itemOrder)

    return result


n = 8
m = 2
group = [-1, -1, 1, 0, 0, 1, 0, -1]
beforeItems = [[], [6], [5], [6], [3, 6], [], [], []]
print(sortItems(n, m, group, beforeItems))

1857. Largest Color Value in a Directed Graph¶

LeetCode | LeetCode CH (Hard)
Tags: hash table, dynamic programming, graph, topological sort, memoization, counting

1857. Largest Color Value in a Directed Graph - Python Solution

from collections import defaultdict, deque
from typing import List


# Topological Sort
def largestPathValue(colors: str, edges: List[List[int]]) -> int:
    n = len(colors)
    graph = defaultdict(list)
    indegree = [0 for _ in range(n)]

    for u, v in edges:
        graph[u].append(v)
        indegree[v] += 1

    q = deque([i for i in range(n) if indegree[i] == 0])

    dp = [[0] * 26 for _ in range(n)]

    for i in range(n):
        dp[i][ord(colors[i]) - ord("a")] = 1

    processed, max_color = 0, 0

    while q:
        n1 = q.popleft()
        processed += 1
        max_color = max(max_color, max(dp[n1]))

        for n2 in graph[n1]:
            indegree[n2] -= 1
            for i in range(26):
                dp[n2][i] = max(
                    dp[n2][i],
                    dp[n1][i] + (1 if i == ord(colors[n2]) - ord("a") else 0),
                )
            if indegree[n2] == 0:
                q.append(n2)

    return max_color if processed == n else -1


colors = "abaca"
edges = [[0, 1], [0, 2], [2, 3], [3, 4]]
print(largestPathValue(colors, edges))  # 3