Standard Traversal

Table of Contents

• 547. Number of Provinces (Medium)
• 802. Find Eventual Safe States (Medium)
• 841. Keys and Rooms (Medium)
• 1129. Shortest Path with Alternating Colors (Medium)
• 1376. Time Needed to Inform All Employees (Medium)
• 1466. Reorder Routes to Make All Paths Lead to the City Zero (Medium)
• 797. All Paths From Source to Target (Medium)
• 1192. Critical Connections in a Network (Hard)

547. Number of Provinces

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, union find, graph

• Return the number of provinces.

Union Find

• Find by Path Compression
• Union by Rank
• Time Complexity: O(log(n))
• Space Complexity: O(n)

template/union_find.py

class UnionFind:
    def __init__(self, n):
        self.par = {i: i for i in range(n)}
        self.rank = {i: 1 for i in range(n)}

    def find(self, n):
        p = self.par[n]
        while self.par[p] != p:
            self.par[p] = self.par[self.par[p]]
            p = self.par[p]
        return p

    def union(self, n1, n2):
        p1, p2 = self.find(n1), self.find(n2)

        if p1 == p2:
            return None

        if self.rank[p1] > self.rank[p2]:
            self.par[p2] = p1
        elif self.rank[p1] < self.rank[p2]:
            self.par[p1] = p2
        else:
            self.par[p2] = p1
            self.rank[p1] += 1

    def connected(self, n1, n2):
        return self.find(n1) == self.find(n2)

547. Number of Provinces - Python Solution

from collections import defaultdict, deque
from typing import List

from template import UnionFind


# DFS (Adjacency Matrix)
def findCircleNumDFSMatrix(isConnected: List[List[int]]) -> int:
    n = len(isConnected)
    visited = set()

    def dfs(node):
        if node in visited:
            return
        visited.add(node)
        for neighbor in range(n):
            if node != neighbor and isConnected[node][neighbor] == 1:
                dfs(neighbor)

    res = 0
    for i in range(n):
        if i not in visited:
            dfs(i)
            res += 1

    return res


# DFS (Adjacency List)
def findCircleNumDFSList(isConnected: List[List[int]]) -> int:
    graph = defaultdict(list)
    n = len(isConnected)

    for i in range(n):
        for j in range(i + 1, n):
            if isConnected[i][j] == 1:
                graph[i].append(j)
                graph[j].append(i)

    visited = set()

    def dfs(node):
        if node in visited:
            return
        visited.add(node)
        for neighbor in graph[node]:
            dfs(neighbor)

    res = 0
    for i in range(n):
        if i not in visited:
            dfs(i)
            res += 1

    return res


# BFS (Adjacency Matrix)
def findCircleNumBFS(isConnected: List[List[int]]) -> int:
    n = len(isConnected)
    visited = set()
    q = deque()
    res = 0

    for i in range(n):
        if i not in visited:
            res += 1

            q.append(i)
            while q:
                node = q.popleft()
                visited.add(node)
                for node, val in enumerate(isConnected[node]):
                    if val == 1 and node not in visited:
                        q.append(node)
                        visited.add(node)

    return res


# Union Find
def findCircleNumUF(isConnected: List[List[int]]) -> int:
    n = len(isConnected)
    uf = UnionFind(n)

    for i in range(n):
        for j in range(i + 1, n):
            if isConnected[i][j] == 1:
                uf.union(i, j)

    res = len(set(uf.find(i) for i in range(n)))

    return res


# Union Find
def findCircleNum(isConnected: List[List[int]]) -> int:
    n = len(isConnected)
    par = {i: i for i in range(n)}
    rank = {i: 0 for i in range(n)}

    def find(n):
        p = par[n]
        while par[p] != p:
            par[p] = par[par[p]]
            p = par[p]
        return p

    def union(n1, n2):
        p1, p2 = find(n1), find(n2)

        if p1 == p2:
            return None

        if rank[p1] > rank[p2]:
            par[p2] = p1
        elif rank[p1] < rank[p2]:
            par[p1] = p2
        else:
            par[p2] = p1
            rank[p1] += 1

    for i in range(n):
        for j in range(i + 1, n):
            if isConnected[i][j] == 1:
                union(i, j)

    res = len(set(find(i) for i in range(n)))

    return res


isConnected = [[1, 1, 0], [1, 1, 0], [0, 0, 1]]
print(findCircleNumDFSList(isConnected))  # 2
print(findCircleNumDFSMatrix(isConnected))  # 2
print(findCircleNumBFS(isConnected))  # 2
print(findCircleNum(isConnected))  # 2
print(findCircleNumUF(isConnected))  # 2

802. Find Eventual Safe States

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

802. Find Eventual Safe States - Python Solution

from collections import defaultdict, deque
from typing import List


# Topological Sort
def eventualSafeNodesTS(graph: List[List[int]]) -> List[int]:
    n = len(graph)
    reverse_graph = defaultdict(list)
    indegree = [0 for _ in range(n)]
    safe = [False for _ in range(n)]

    for u in range(n):
        for v in graph[u]:
            reverse_graph[v].append(u)
        indegree[u] = len(graph[u])

    q = deque([i for i in range(n) if indegree[i] == 0])

    while q:
        node = q.popleft()
        safe[node] = True

        for neighbor in reverse_graph[node]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                q.append(neighbor)

    return [i for i in range(n) if safe[i]]


# DFS
def eventualSafeNodesDFS(graph: List[List[int]]) -> List[int]:
    n = len(graph)
    state = [0 for _ in range(n)]  # 0: unvisited, 1: visiting, 2: visited

    def dfs(node):
        if state[node] > 0:
            return state[node] == 2
        state[node] = 1
        for neighbor in graph[node]:
            if state[neighbor] == 1 or not dfs(neighbor):
                return False
        state[node] = 2
        return True

    return [i for i in range(n) if dfs(i)]


graph = [[1, 2], [2, 3], [5], [0], [5], [], []]
print(eventualSafeNodesTS(graph))  # [2, 4, 5, 6]
print(eventualSafeNodesDFS(graph))  # [2, 4, 5, 6]

841. Keys and Rooms

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph

841. Keys and Rooms - Python Solution

from collections import deque
from typing import List


# DFS
def canVisitAllRoomsDFS(rooms: List[List[int]]) -> bool:
    n = len(rooms)
    visited = [False for _ in range(n)]

    def dfs(room):
        visited[room] = True
        for key in rooms[room]:
            if not visited[key]:
                dfs(key)

    dfs(0)

    return all(visited)


# BFS
def canVisitAllRoomsBFS(rooms):
    n = len(rooms)
    visited = [False for _ in range(n)]
    q = deque([0])
    visited[0] = True

    while q:
        room = q.popleft()
        for key in rooms[room]:
            if not visited[key]:
                visited[key] = True
                q.append(key)

    return all(visited)


rooms = [[1, 3], [3, 0, 1], [2], [0]]
print(canVisitAllRoomsDFS(rooms))  # False
print(canVisitAllRoomsBFS(rooms))  # False

1129. Shortest Path with Alternating Colors

• LeetCode | LeetCode CH (Medium)

• Tags: breadth first search, graph

1129. Shortest Path with Alternating Colors - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS
def shortestAlternatingPaths(
    n: int, redEdges: List[List[int]], blueEdges: List[List[int]]
) -> List[int]:
    red_graph = defaultdict(list)
    blue_graph = defaultdict(list)

    for u, v in redEdges:
        red_graph[u].append(v)
    for u, v in blueEdges:
        blue_graph[u].append(v)

    answer = [-1 for _ in range(n)]
    q = deque([(0, 0, 0), (0, 0, 1)])  # (node, distance, color)
    visited = set()

    while q:
        node, dist, color = q.popleft()
        if (node, color) in visited:
            continue
        visited.add((node, color))
        if answer[node] == -1:
            answer[node] = dist
        if color == 0:
            for neighbor in blue_graph[node]:
                q.append((neighbor, dist + 1, 1))
        else:
            for neighbor in red_graph[node]:
                q.append((neighbor, dist + 1, 0))

    return answer


n = 3
red_edges = [[0, 1], [1, 2]]
blue_edges = []
print(shortestAlternatingPaths(n, red_edges, blue_edges))  # [0, 1, -1]

1376. Time Needed to Inform All Employees

• LeetCode | LeetCode CH (Medium)

• Tags: tree, depth first search, breadth first search

1376. Time Needed to Inform All Employees - Python Solution

from collections import defaultdict, deque
from typing import List


# DFS
def numOfMinutesDFS(
    n: int, headID: int, manager: List[int], informTime: List[int]
) -> int:
    graph = defaultdict(list)
    for i in range(n):
        if manager[i] != -1:
            graph[manager[i]].append(i)

    def dfs(node):
        time = 0
        for sub in graph[node]:
            time = max(time, dfs(sub))
        return time + informTime[node]

    return dfs(headID)


# BFS
def numOfMinutesBFS(
    n: int, headID: int, manager: List[int], informTime: List[int]
) -> int:
    graph = defaultdict(list)
    for i in range(n):
        if manager[i] != -1:
            graph[manager[i]].append(i)

    q = deque([(headID, 0)])
    max_time = 0

    while q:
        node, time = q.popleft()
        max_time = max(max_time, time)
        for sub in graph[node]:
            q.append((sub, time + informTime[node]))

    return max_time


n = 6
headID = 2
manager = [2, 2, -1, 2, 2, 2]
informTime = [0, 0, 1, 0, 0, 0]
print(numOfMinutesDFS(n, headID, manager, informTime))  # 1
print(numOfMinutesBFS(n, headID, manager, informTime))  # 1

1466. Reorder Routes to Make All Paths Lead to the City Zero

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph

• 

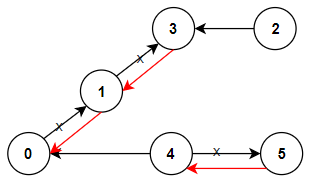
1466. Reorder Routes to Make All Paths Lead to the City Zero - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS
def minReorderBFS(n: int, connections: List[List[int]]) -> int:
    graph = defaultdict(list)
    for u, v in connections:
        graph[u].append((v, 1))  # go
        graph[v].append((u, 0))  # come

    changes = 0
    q = deque([(0, -1)])

    while q:
        n1, d1 = q.popleft()

        for n2, d2 in graph[n1]:
            if n2 != d1:
                changes += d2
                q.append((n2, n1))

    return changes


# DFS
def minReorderDFS(n: int, connections: List[List[int]]) -> int:
    graph = defaultdict(list)
    for u, v in connections:
        graph[u].append((v, 1))  # go
        graph[v].append((u, 0))  # come

    def dfs(n1, d1):
        changes = 0
        for n2, d2 in graph[n1]:
            if n2 != d1:
                changes += d2 + dfs(n2, n1)
        return changes

    return dfs(0, -1)


n = 5
connections = [[1, 0], [1, 2], [3, 2], [3, 4]]
print(minReorderBFS(n, connections))  # 2
print(minReorderDFS(n, connections))  # 2

797. All Paths From Source to Target

• LeetCode | LeetCode CH (Medium)

• Tags: backtracking, depth first search, breadth first search, graph

797. All Paths From Source to Target - Python Solution

from collections import deque
from typing import List


# DFS (Backtracking)
def allPathsSourceTargetDFS(graph: List[List[int]]) -> List[List[int]]:
    res = []
    n = len(graph)

    def dfs(node, path):
        if node == n - 1:
            res.append(path.copy())
            return None

        for nei in graph[node]:
            path.append(nei)
            dfs(nei, path)
            path.pop()

    dfs(0, [0])

    return res


# BFS
def allPathsSourceTargetBFS(graph: List[List[int]]) -> List[List[int]]:
    n = len(graph)
    res = []
    q = deque([(0, [0])])

    while q:
        node, path = q.popleft()

        if node == n - 1:
            res.append(path)

        for nei in graph[node]:
            q.append((nei, path + [nei]))

    return res


graph = [[1, 2], [3], [3], []]
print(allPathsSourceTargetDFS(graph))  # [[0, 1, 3], [0, 2, 3]]
print(allPathsSourceTargetBFS(graph))  # [[0, 1, 3], [0, 2, 3]]

1192. Critical Connections in a Network

• LeetCode | LeetCode CH (Hard)

• Tags: depth first search, graph, biconnected component

1192. Critical Connections in a Network - Python Solution

from collections import defaultdict
from typing import List


# Tarjan
def criticalConnections(
    n: int, connections: List[List[int]]
) -> List[List[int]]:
    graph = defaultdict(list)
    for u, v in connections:
        graph[u].append(v)
        graph[v].append(u)

    disc = [-1] * n
    low = [-1] * n
    bridges = []
    time = 0

    def dfs(n1, prev):
        nonlocal time
        disc[n1], low[n1] = time, time
        time += 1

        for n2 in graph[n1]:
            if n2 == prev:
                continue
            if disc[n2] == -1:
                dfs(n2, n1)
                low[n1] = min(low[n1], low[n2])

                if low[n2] > disc[n1]:
                    bridges.append([n1, n2])
            else:
                low[n1] = min(low[n1], disc[n2])

    for i in range(n):
        if disc[i] == -1:
            dfs(i, -1)

    return bridges


n = 4
connections = [[0, 1], [1, 2], [2, 0], [1, 3]]
print(criticalConnections(n, connections))  # [[1, 3]]

Comments