Skip to content

Graph Theory

Resources

Concepts

  • Graph
  • Vertex (Node)
  • Edge
  • Weight

Types

  • Undirected graph: A graph in which edges have no direction.

undirected_graph

  • Directed graph: A graph in which edges have direction.
flowchart LR
A((1)) --> B((2)) & C((3))
C --> B & D((4))
D --> C
  • Cyclic graph: A graph in which there is a cycle. A cycle is a path of edges that starts and ends at the same vertex, e.g., 1 -> 3 -> 4 -> 1.
flowchart LR
A((1)) --> B((2)) & C((3))
B --> C
C --> D((4))
D --> A
  • Acyclic graph: A graph in which there is no cycle.

acyclic_graph

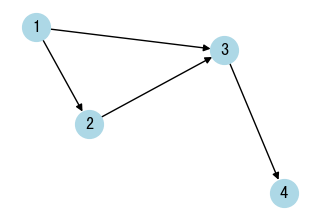
  • Directed Acyclic Graph (DAG): A directed graph with no cycles.
  • Topological sort

dag

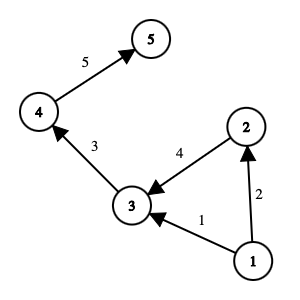
  • Weighted graph: A graph in which edges have weights.

weighted

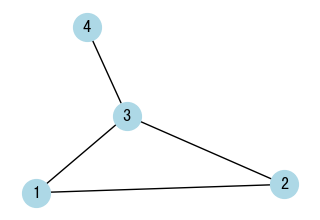
  • Connected Graph: A graph in which there is a path between every pair of vertices.

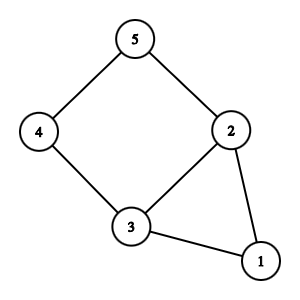
connected

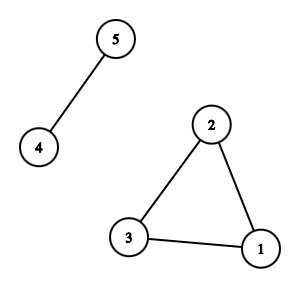
  • Disconnected Graph: A graph in which there is no path between some pairs of vertices.

disconnected

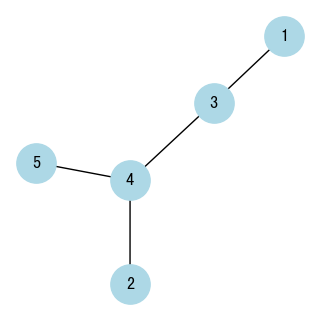
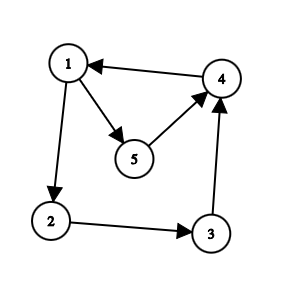
  • Eulerian path: A path that visits every edge exactly once, e.g., 5 -> 4 -> 1 -> 2 -> 3.

eulerian

Representation

  1. Adjacency Matrix
  2. Adjacency List
flowchart LR
1((1))
2((2))
3((3))
4((4))
1 --> 3
1 --> 2
3 --> 4
2 --> 3

Adjacency Matrix

Node 1 Node 2 Node 3 Node 4
Node 1 0 1 1 0
Node 2 0 0 1 0
Node 3 0 0 0 1
Node 4 0 0 0 0 
grid = [
    [0, 1, 1, 0],
    [0, 0, 1, 0],
    [0, 0, 0, 1],
    [0, 0, 0, 0]
]

Adjacency List

classDiagram
direction LR
class 1{2, 3}
class 2{3}
class 3{4}
class 4{-}
1 -- 2
2 -- 3
3 -- 4
graph = {
    1: [2, 3],
    2: [3],
    3: [4],
    4: []
}

Degree

  1. Degree: Number of edges connected to a node
  2. In-degree: Number of edges coming into a node
  3. Out-degree: Number of edges going out of a node
flowchart LR
1((1))
2((2))
3((3))
4((4))
1 --> 3
1 --> 2
3 --> 4
2 --> 3
  • In-degree of Node 1: 0
  • Out-degree of Node 1: 2
  • In-degree of Node 2: 1
  • Out-degree of Node 2: 1
# List
in_degree = [0, 1, 2, 1]
out_degree = [2, 1, 1, 0]

# Dict
in_degree = {1: 0, 2: 1, 3: 2, 4: 1}
out_degree = {1: 2, 2: 1, 3: 1, 4: 0}

Graph - Bellman-Ford Algorithm

  • The Bellman-Ford algorithm is used to find the shortest path from a source vertex to all other vertices in a weighted graph.
  • It is slower than Dijkstra's algorithm, but it is more versatile, as it is able to handle graphs with negative edge weights.
  • Time Complexity: O(V x E), where V is the number of vertices and E is the number of edges in the graph.
  • Space Complexity: O(V), where V is the number of vertices in the graph.