Topological Sorting

Table of Contents

• 1557. Minimum Number of Vertices to Reach All Nodes (Medium)
• 210. Course Schedule II (Medium)
• 1462. Course Schedule IV (Medium)
• 2115. Find All Possible Recipes from Given Supplies (Medium)
• 851. Loud and Rich (Medium)
• 310. Minimum Height Trees (Medium)
• 2392. Build a Matrix With Conditions (Hard)
• 802. Find Eventual Safe States (Medium)
• 1591. Strange Printer II (Hard)
• 1203. Sort Items by Groups Respecting Dependencies (Hard)
• 2603. Collect Coins in a Tree (Hard)
• 269. Alien Dictionary (Hard) 👑
• 444. Sequence Reconstruction (Medium) 👑
• 1059. All Paths from Source Lead to Destination (Medium) 👑
• 1136. Parallel Courses (Medium) 👑

1557. Minimum Number of Vertices to Reach All Nodes

• LeetCode | LeetCode CH (Medium)

• Tags: graph

• Return a list of integers representing the minimum number of vertices needed to traverse all the nodes.
• ✅ Return the vertices with indegree 0.

• edges = [[0, 1], [0, 2], [2, 5], [3, 4], [4, 2]]
• Initialization

src	0	0	2	3	4
dst	1	2	5	4	2
node	0	1	2	3	4	5
in-degree	0	0	0	0	0	0

src	0	0	2	3	4
dst	1	2	5	4	2
node	0	1	2	3	4	5
in-degree	0	1	0	0	0	0

src	0	0	2	3	4
dst	1	2	5	4	2
node	0	1	2	3	4	5
in-degree	0	1	1	0	0	0

src	0	0	2	3	4
dst	1	2	5	4	2
node	0	1	2	3	4	5
in-degree	0	1	1	0	0	1

src	0	0	2	3	4
dst	1	2	5	4	2
node	0	1	2	3	4	5
in-degree	0	1	1	0	1	1

src	0	0	2	3	4
dst	1	2	5	4	2
node	0	1	2	3	4	5
in-degree	0	1	2	0	1	1

1557. Minimum Number of Vertices to Reach All Nodes - Python Solution

from typing import List


# Graph
def findSmallestSetOfVertices(n: int, edges: List[List[int]]) -> List[int]:
    indegree = {i: 0 for i in range(n)}

    for a, b in edges:
        indegree[b] += 1

    return [i for i in range(n) if indegree[i] == 0]


n = 6
edges = [[0, 1], [0, 2], [2, 5], [3, 4], [4, 2]]
print(findSmallestSetOfVertices(n, edges))  # [0, 3]

210. Course Schedule II

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

• Return the ordering of courses you should take to finish all courses. If there are multiple valid answers, return any of them.

210. Course Schedule II - Python Solution

from collections import defaultdict, deque
from typing import List


# 1. BFS - Kahn's Algorithm
def findOrderBFS(numCourses: int, prerequisites: List[List[int]]) -> List[int]:
    graph = defaultdict(list)
    indegree = defaultdict(int)

    for crs, pre in prerequisites:
        graph[pre].append(crs)
        indegree[crs] += 1

    q = deque([i for i in range(numCourses) if indegree[i] == 0])
    order = []

    while q:
        pre = q.popleft()
        order.append(pre)

        for crs in graph[pre]:
            indegree[crs] -= 1
            if indegree[crs] == 0:
                q.append(crs)

    return order if len(order) == numCourses else []


# 2. DFS + Set
def findOrderDFS1(
    numCourses: int, prerequisites: List[List[int]]
) -> List[int]:
    adj = defaultdict(list)
    for crs, pre in prerequisites:
        adj[crs].append(pre)

    visit, cycle = set(), set()
    order = []

    def dfs(crs):
        if crs in cycle:
            return False
        if crs in visit:
            return True

        cycle.add(crs)
        for pre in adj[crs]:
            if not dfs(pre):
                return False

        cycle.remove(crs)
        visit.add(crs)
        order.append(crs)
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return []

    return order


# 3. DFS + List
def findOrderDFS2(
    numCourses: int, prerequisites: List[List[int]]
) -> List[int]:
    adj = defaultdict(list)
    for pre, crs in prerequisites:
        adj[crs].append(pre)

    # 0: not visited, 1: visiting, 2: visited
    state = [0] * numCourses
    order = []

    def dfs(crs):
        if state[crs] == 1:
            return False
        if state[crs] == 2:
            return True

        state[crs] = 1

        for pre in adj[crs]:
            if not dfs(pre):
                return False

        state[crs] = 2
        order.append(crs)
        return True

    for crs in range(numCourses):
        if not dfs(crs):
            return []

    return order[::-1]


numCourses = 5
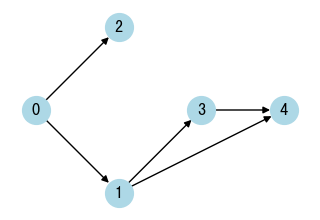
prerequisites = [[0, 1], [0, 2], [1, 3], [1, 4], [3, 4]]
print(findOrderBFS(numCourses, prerequisites))  # [2, 4, 3, 1, 0]
print(findOrderDFS1(numCourses, prerequisites))  # [4, 3, 1, 2, 0]
print(findOrderDFS2(numCourses, prerequisites))  # [4, 3, 2, 1, 0]

210. Course Schedule II - C++ Solution

#include <iostream>
#include <queue>
#include <vector>
using namespace std;

class Solution {
   public:
    // BFS
    vector<int> findOrderBFS(int numCourses,
                             vector<vector<int>> &prerequisites) {
        vector<vector<int>> graph(numCourses);
        vector<int> indegree(numCourses, 0);

        for (auto &pre : prerequisites) {
            graph[pre[1]].push_back(pre[0]);
            indegree[pre[0]]++;
        }

        queue<int> q;
        for (int i = 0; i < numCourses; i++)
            if (indegree[i] == 0) q.push(i);

        vector<int> order;

        while (!q.empty()) {
            int cur = q.front();
            q.pop();
            order.push_back(cur);

            for (int nxt : graph[cur]) {
                indegree[nxt]--;
                if (indegree[nxt] == 0) q.push(nxt);
            }
        }

        return (int)order.size() == numCourses ? order : vector<int>{};
    }
};

int main() {
    Solution obj;
    vector<vector<int>> prerequisites{{1, 0}, {2, 0}, {3, 1}, {3, 2}};
    vector<int> res = obj.findOrderBFS(4, prerequisites);
    for (size_t i = 0; i < res.size(); i++) cout << res[i] << "\n";
    return 0;
}

1462. Course Schedule IV

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

2115. Find All Possible Recipes from Given Supplies

• LeetCode | LeetCode CH (Medium)

• Tags: array, hash table, string, graph, topological sort

851. Loud and Rich

• LeetCode | LeetCode CH (Medium)

• Tags: array, depth first search, graph, topological sort

310. Minimum Height Trees

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

310. Minimum Height Trees - Python Solution

from collections import deque
from typing import List


def findMinHeightTrees(n: int, edges: List[List[int]]) -> List[int]:
    if n == 1:
        return [0]

    graph = {i: set() for i in range(n)}
    for u, v in edges:
        graph[u].add(v)
        graph[v].add(u)

    q = deque([i for i in range(n) if len(graph[i]) == 1])
    remaining = n

    while remaining > 2:
        size = len(q)
        remaining -= size

        for _ in range(size):
            cur = q.popleft()
            nei = graph[cur].pop()
            graph[nei].remove(cur)

            if len(graph[nei]) == 1:
                q.append(nei)

    return list(q)


n = 6
edges = [[3, 0], [3, 1], [3, 2], [3, 4], [5, 4]]
print(findMinHeightTrees(n, edges))  # [3, 4]

2392. Build a Matrix With Conditions

• LeetCode | LeetCode CH (Hard)

• Tags: array, graph, topological sort, matrix

802. Find Eventual Safe States

• LeetCode | LeetCode CH (Medium)

• Tags: depth first search, breadth first search, graph, topological sort

802. Find Eventual Safe States - Python Solution

from collections import defaultdict, deque
from typing import List


# Topological Sort
def eventualSafeNodesTS(graph: List[List[int]]) -> List[int]:
    n = len(graph)
    reverse_graph = defaultdict(list)
    indegree = [0 for _ in range(n)]
    safe = [False for _ in range(n)]

    for u in range(n):
        for v in graph[u]:
            reverse_graph[v].append(u)
        indegree[u] = len(graph[u])

    q = deque([i for i in range(n) if indegree[i] == 0])

    while q:
        node = q.popleft()
        safe[node] = True

        for neighbor in reverse_graph[node]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                q.append(neighbor)

    return [i for i in range(n) if safe[i]]


# DFS
def eventualSafeNodesDFS(graph: List[List[int]]) -> List[int]:
    n = len(graph)
    state = [0 for _ in range(n)]  # 0: unvisited, 1: visiting, 2: visited

    def dfs(node):
        if state[node] > 0:
            return state[node] == 2
        state[node] = 1
        for neighbor in graph[node]:
            if state[neighbor] == 1 or not dfs(neighbor):
                return False
        state[node] = 2
        return True

    return [i for i in range(n) if dfs(i)]


graph = [[1, 2], [2, 3], [5], [0], [5], [], []]
print(eventualSafeNodesTS(graph))  # [2, 4, 5, 6]
print(eventualSafeNodesDFS(graph))  # [2, 4, 5, 6]

1591. Strange Printer II

• LeetCode | LeetCode CH (Hard)

• Tags: array, graph, topological sort, matrix

1203. Sort Items by Groups Respecting Dependencies

• LeetCode | LeetCode CH (Hard)

• Tags: depth first search, breadth first search, graph, topological sort

• Return any permutation of the items that satisfies the requirements.

1203. Sort Items by Groups Respecting Dependencies - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS - Kahn's algorithm (Topological Sort)
def sortItems(
    n: int, m: int, group: List[int], beforeItems: List[List[int]]
) -> List[int]:
    def topological_sort(graph, indegree, nodes):
        q = deque([node for node in nodes if indegree[node] == 0])
        result = []

        while q:
            node = q.popleft()
            result.append(node)

            for neighbor in graph[node]:
                indegree[neighbor] -= 1
                if indegree[neighbor] == 0:
                    q.append(neighbor)

        return result if len(result) == len(nodes) else []

    groupItems = defaultdict(list)
    groupGraph = defaultdict(set)
    groupIndegree = defaultdict(int)
    itemGraph = defaultdict(set)
    itemIndegree = defaultdict(int)

    for i in range(n):
        if group[i] == -1:
            group[i] = m
            m += 1
        groupItems[group[i]].append(i)

    for i, beforeItem in enumerate(beforeItems):
        for before in beforeItem:
            if group[before] != group[i]:
                if group[i] not in groupGraph[group[before]]:
                    groupGraph[group[before]].add(group[i])
                    groupIndegree[group[i]] += 1
            else:
                itemGraph[before].add(i)
                itemIndegree[i] += 1

    allGroups = list(set(group))
    groupOrder = topological_sort(groupGraph, groupIndegree, allGroups)
    if not groupOrder:
        return []

    result = []
    for g in groupOrder:
        items = groupItems[g]
        itemOrder = topological_sort(itemGraph, itemIndegree, items)
        if not itemOrder:
            return []
        result.extend(itemOrder)

    return result


n = 8
m = 2
group = [-1, -1, 1, 0, 0, 1, 0, -1]
beforeItems = [[], [6], [5], [6], [3, 6], [], [], []]
print(sortItems(n, m, group, beforeItems))

2603. Collect Coins in a Tree

• LeetCode | LeetCode CH (Hard)

• Tags: array, tree, graph, topological sort

269. Alien Dictionary

• LeetCode | LeetCode CH (Hard)

• Tags: array, string, depth first search, breadth first search, graph, topological sort

• Return the correct order of characters in the alien language.

269. Alien Dictionary - Python Solution

from collections import defaultdict, deque
from typing import List


# BFS - Kahn's algorithm (Topological Sort)
def alienOrderBFS(words: List[str]) -> str:
    graph = defaultdict(set)
    indegree = {c: 0 for word in words for c in word}

    for i in range(len(words) - 1):
        w1, w2 = words[i], words[i + 1]
        minLen = min(len(w1), len(w2))

        if len(w1) > len(w2) and w1[:minLen] == w2[:minLen]:
            return ""

        for j in range(minLen):
            if w1[j] != w2[j]:
                if w2[j] not in graph[w1[j]]:
                    graph[w1[j]].add(w2[j])
                    indegree[w2[j]] += 1
                break

    q = deque([c for c in indegree if indegree[c] == 0])
    result = []

    while q:
        char = q.popleft()
        result.append(char)

        for neighbor in graph[char]:
            indegree[neighbor] -= 1
            if indegree[neighbor] == 0:
                q.append(neighbor)

    return "".join(result) if len(result) == len(indegree) else ""


# DFS - Topological Sort
def alienOrderDFS(words: List[str]) -> str:
    graph = defaultdict(set)
    visited = {}
    result = []

    for i in range(len(words) - 1):
        w1, w2 = words[i], words[i + 1]
        minLen = min(len(w1), len(w2))

        if len(w1) > len(w2) and w1[:minLen] == w2[:minLen]:
            return ""

        for j in range(minLen):
            if w1[j] != w2[j]:
                if w2[j] not in graph[w1[j]]:
                    graph[w1[j]].add(w2[j])
                break

    def dfs(c):
        if c in visited:
            return visited[c]

        visited[c] = False
        for neighbor in graph[c]:
            if not dfs(neighbor):
                return False

        visited[c] = True
        result.append(c)
        return True

    for c in list(graph.keys()):
        if not dfs(c):
            return ""

    return "".join(result[::-1])


words = ["wrt", "wrf", "er", "ett", "rftt"]
print(alienOrderBFS(words))  # wertf
print(alienOrderDFS(words))  # wertf

444. Sequence Reconstruction

• LeetCode | LeetCode CH (Medium)

• Tags: array, graph, topological sort

1059. All Paths from Source Lead to Destination

• LeetCode | LeetCode CH (Medium)

• Tags: graph, topological sort

1136. Parallel Courses

• LeetCode | LeetCode CH (Medium)

• Tags: graph, topological sort

• Return the minimum number of semesters needed to take all courses.

1136. Parallel Courses - Python Solution

from collections import deque
from typing import List


# Topological Sort
def minimumSemesters(n: int, relations: List[List[int]]) -> int:
    graph = {i: [] for i in range(1, n + 1)}
    indegree = {i: 0 for i in range(1, n + 1)}

    for pre, nxt in relations:
        graph[pre].append(nxt)
        indegree[nxt] += 1

    q = deque([i for i in range(1, n + 1) if indegree[i] == 0])
    semester = 0
    done = 0

    while q:
        semester += 1
        size = len(q)

        for _ in range(size):
            pre = q.popleft()
            done += 1

            for nxt in graph[pre]:
                indegree[nxt] -= 1
                if indegree[nxt] == 0:
                    q.append(nxt)

    return semester if done == n else -1


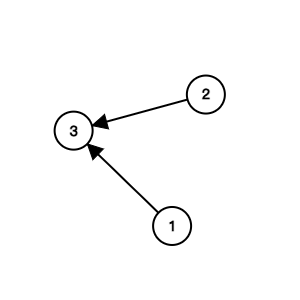
n = 3
relations = [[1, 3], [2, 3]]
print(minimumSemesters(n, relations))  # 2

Comments