Shortest Path Single Source Dijkstra¶
Table of Contents¶
- 743. Network Delay Time (Medium)
- 3341. Find Minimum Time to Reach Last Room I (Medium)
- 3112. Minimum Time to Visit Disappearing Nodes (Medium)
- 2642. Design Graph With Shortest Path Calculator (Hard)
- 1514. Path with Maximum Probability (Medium)
- 3342. Find Minimum Time to Reach Last Room II (Medium)
- 1631. Path With Minimum Effort (Medium)
- 1786. Number of Restricted Paths From First to Last Node (Medium)
- 3123. Find Edges in Shortest Paths (Hard)
- 1976. Number of Ways to Arrive at Destination (Medium)
- 778. Swim in Rising Water (Hard)
- 2662. Minimum Cost of a Path With Special Roads (Medium)
- 3377. Digit Operations to Make Two Integers Equal (Medium)
- 2045. Second Minimum Time to Reach Destination (Hard)
- 3419. Minimize the Maximum Edge Weight of Graph (Medium)
- 882. Reachable Nodes In Subdivided Graph (Hard)
- 2203. Minimum Weighted Subgraph With the Required Paths (Hard)
- 2577. Minimum Time to Visit a Cell In a Grid (Hard)
- 1928. Minimum Cost to Reach Destination in Time (Hard)
- 787. Cheapest Flights Within K Stops (Medium)
- 2699. Modify Graph Edge Weights (Hard)
- 1810. Minimum Path Cost in a Hidden Grid (Medium) 👑
- 2093. Minimum Cost to Reach City With Discounts (Medium) 👑
- 2473. Minimum Cost to Buy Apples (Medium) 👑
- 2714. Find Shortest Path with K Hops (Hard) 👑
- 2737. Find the Closest Marked Node (Medium) 👑
743. Network Delay Time¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: depth first search, breadth first search, graph, heap priority queue, shortest path
- Return the minimum time taken to reach all nodes in a network.
graph LR
1((1))
2((2))
3((3))
4((4))
2 --> |1| 1
2 --> |1| 3
3 --> |1| 4- Shortest Path Problem: Find the shortest path between two vertices in a graph.
- Dijkstra's Algorithm
- Shortest path algorithm
- Weighted graph (non-negative weights)
- Data Structure: Heap; Hash Set
- Time Complexity: O(E * logV)
- Space Complexity: O(V)
import heapq
from collections import defaultdict
from typing import List
# Dijkstra - Set
def networkDelayTime1(times: List[List[int]], n: int, k: int) -> int:
graph = defaultdict(list)
for u, v, w in times:
graph[u].append((v, w))
heap = [(0, k)]
visit = set()
t = 0
while heap:
w1, n1 = heapq.heappop(heap)
if n1 in visit:
continue
visit.add(n1)
t = w1
for n2, w2 in graph[n1]:
heapq.heappush(heap, (w1 + w2, n2))
return t if len(visit) == n else -1
# Dijkstra - Dict
def networkDelayTime2(times: List[List[int]], n: int, k: int) -> int:
graph = defaultdict(list)
for u, v, w in times:
graph[u].append((v, w))
heap = [(0, k)]
dist = defaultdict(int)
while heap:
w1, n1 = heapq.heappop(heap)
if n1 in dist:
continue
dist[n1] = w1
for n2, w2 in graph[n1]:
heapq.heappush(heap, (w1 + w2, n2))
return max(dist.values()) if len(dist) == n else -1
# Bellman-Ford
def networkDelayTimeBF(times: List[List[int]], n: int, k: int) -> int:
delay = {i: float("inf") for i in range(1, n + 1)}
delay[k] = 0
for _ in range(n - 1):
for u, v, t in times:
delay[v] = min(delay[v], delay[u] + t)
max_delay = max(delay.values())
return max_delay if max_delay < float("inf") else -1
# |--------------|-----------|--------|
# | Approach | Time | Space |
# |--------------|-----------|--------|
# | Dijkstra | O(E*logV) | O(V+E) |
# | Bellman-Ford | O(E*V) | O(V) |
# |--------------|-----------|--------|
if __name__ == "__main__":
times = [[2, 1, 1], [2, 3, 1], [3, 4, 1]]
n = 4
k = 2
print(networkDelayTime1(times, n, k)) # 2
print(networkDelayTime2(times, n, k)) # 2
print(networkDelayTimeBF(times, n, k)) # 2
3341. Find Minimum Time to Reach Last Room I¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, matrix, shortest path
3112. Minimum Time to Visit Disappearing Nodes¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, shortest path
2642. Design Graph With Shortest Path Calculator¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: graph, design, heap priority queue, shortest path
1514. Path with Maximum Probability¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, shortest path
import heapq
from collections import defaultdict
from typing import List
# Dijkstra - Dict
def maxProbability1(
n: int,
edges: List[List[int]],
succProb: List[float],
start_node: int,
end_node: int,
) -> float:
graph = defaultdict(list)
for i, (u, v) in enumerate(edges):
graph[u].append((v, succProb[i]))
graph[v].append((u, succProb[i]))
heap = [(-1, start_node)]
max_prob = {i: 0.0 for i in range(n)}
max_prob[start_node] = 1.0
while heap:
p1, n1 = heapq.heappop(heap)
if n1 == end_node:
return -p1
for n2, p2 in graph[n1]:
p2 *= -p1
if p2 > max_prob[n2]:
max_prob[n2] = p2
heapq.heappush(heap, (-p2, n2))
return 0.0
# Dijkstra - Set
def maxProbability2(
n: int,
edges: List[List[int]],
succProb: List[float],
start_node: int,
end_node: int,
) -> float:
graph = defaultdict(list)
for i, (u, v) in enumerate(edges):
graph[u].append((v, succProb[i]))
graph[v].append((u, succProb[i]))
heap = [(-1, start_node)]
visited = set()
while heap:
p1, n1 = heapq.heappop(heap)
visited.add(n1)
if n1 == end_node:
return -p1
for n2, p2 in graph[n1]:
if n2 not in visited:
heapq.heappush(heap, (p1 * p2, n2))
return 0.0
# |------------|-----------|-----------|
# | Approach | Time | Space |
# |------------|-----------|-----------|
# | Dijkstra | O(E log V)| O(E) |
# |------------|-----------|-----------|
n = 3
edges = [[0, 1], [1, 2], [0, 2]]
succProb = [0.5, 0.5, 0.2]
start = 0
end = 2
print(maxProbability1(n, edges, succProb, start, end)) # 0.25
print(maxProbability2(n, edges, succProb, start, end)) # 0.25
3342. Find Minimum Time to Reach Last Room II¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, matrix, shortest path
1631. Path With Minimum Effort¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, binary search, depth first search, breadth first search, union find, heap priority queue, matrix
- Return the minimum effort required to travel from the top-left to the bottom-right corner.
import heapq
from typing import List
# Prim
def minimumEffortPath(heights: List[List[int]]) -> int:
m, n = len(heights), len(heights[0])
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
visited = [[False] * n for _ in range(m)]
heap = [(0, 0, 0)] # (effort, row, col)
while heap:
effort, r, c = heapq.heappop(heap)
if visited[r][c]:
continue
if r == m - 1 and c == n - 1:
return effort
visited[r][c] = True
for dr, dc in directions:
nr, nc = r + dr, c + dc
if 0 <= nr < m and 0 <= nc < n and not visited[nr][nc]:
updated = max(effort, abs(heights[r][c] - heights[nr][nc]))
heapq.heappush(heap, (updated, nr, nc))
return -1
heights = [[1, 2, 2], [3, 8, 2], [5, 3, 5]]
print(minimumEffortPath(heights)) # 2
1786. Number of Restricted Paths From First to Last Node¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: dynamic programming, graph, topological sort, heap priority queue, shortest path
3123. Find Edges in Shortest Paths¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: depth first search, breadth first search, graph, heap priority queue, shortest path
1976. Number of Ways to Arrive at Destination¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: dynamic programming, graph, topological sort, shortest path
import heapq
from typing import List
# Dijkstra
def countPaths(n: int, roads: List[List[int]]) -> int:
mod = 10**9 + 7
graph = [[] for _ in range(n)]
for u, v, w in roads:
graph[u].append((v, w))
graph[v].append((u, w))
dist = [float("inf") for _ in range(n)]
dist[0] = 0
count = [0 for _ in range(n)]
count[0] = 1
heap = [(0, 0)]
while heap:
d, u = heapq.heappop(heap)
if d > dist[u]:
continue
for v, w in graph[u]:
if dist[u] + w < dist[v]:
dist[v] = dist[u] + w
count[v] = count[u]
heapq.heappush(heap, (dist[v], v))
elif dist[u] + w == dist[v]:
count[v] += count[u]
count[v] %= mod
return count[-1]
n = 7
roads = [
[0, 6, 7],
[0, 1, 2],
[1, 2, 3],
[1, 3, 3],
[6, 3, 3],
[3, 5, 1],
[6, 5, 1],
[2, 5, 1],
[0, 4, 5],
[4, 6, 2],
]
print(countPaths(n, roads)) # 4
778. Swim in Rising Water¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: array, binary search, depth first search, breadth first search, union find, heap priority queue, matrix
- Return the minimum time when you can reach the target.
import heapq
from typing import List
# Dijkstra's
def swimInWater(grid: List[List[int]]) -> int:
n = len(grid)
visited = set()
minHeap = [(grid[0][0], 0, 0)]
directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]
visited.add((0, 0))
while minHeap:
time, r, c = heapq.heappop(minHeap)
if r == n - 1 and c == n - 1:
return time
for dr, dc in directions:
nr, nc = r + dr, c + dc
if nr in range(n) and nc in range(n) and (nr, nc) not in visited:
visited.add((nr, nc))
heapq.heappush(minHeap, (max(time, grid[nr][nc]), nr, nc))
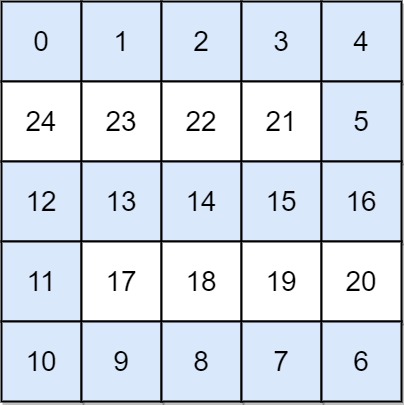
grid = [
[0, 1, 2, 3, 4],
[24, 23, 22, 21, 5],
[12, 13, 14, 15, 16],
[11, 17, 18, 19, 20],
[10, 9, 8, 7, 6],
]
print(swimInWater(grid)) # 16
2662. Minimum Cost of a Path With Special Roads¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, shortest path
3377. Digit Operations to Make Two Integers Equal¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: math, graph, heap priority queue, number theory, shortest path
2045. Second Minimum Time to Reach Destination¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: breadth first search, graph, shortest path
3419. Minimize the Maximum Edge Weight of Graph¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: binary search, depth first search, breadth first search, graph, shortest path
882. Reachable Nodes In Subdivided Graph¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: graph, heap priority queue, shortest path
import heapq
from typing import List
# Dijkstra's
def reachableNodes(self, edges: List[List[int]], maxMoves: int, n: int) -> int:
graph = {i: {} for i in range(n)}
for u, v, cnt in edges:
graph[u][v] = cnt
graph[v][u] = cnt
heap = [(-maxMoves, 0)]
seen = {}
while heap:
moves, node = heapq.heappop(heap)
if node in seen:
continue
seen[node] = -moves
for nxt, cnt in graph[node].items():
movesLeft = -moves - cnt - 1
if nxt not in seen and movesLeft >= 0:
heapq.heappush(heap, (-movesLeft, nxt))
res = len(seen)
for u, v, cnt in edges:
res += min(seen.get(u, 0) + seen.get(v, 0), cnt)
return res
edges = [[0, 1, 10], [0, 2, 1], [1, 2, 2]]
maxMoves = 6
n = 3
print(reachableNodes(None, edges, maxMoves, n)) # 13
2203. Minimum Weighted Subgraph With the Required Paths¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: graph, shortest path
2577. Minimum Time to Visit a Cell In a Grid¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: array, breadth first search, graph, heap priority queue, matrix, shortest path
1928. Minimum Cost to Reach Destination in Time¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: array, dynamic programming, graph
787. Cheapest Flights Within K Stops¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: dynamic programming, depth first search, breadth first search, graph, heap priority queue, shortest path
- Return the cheapest price from
srctodstwith at mostKstops.
graph TD
0((0))
1((1))
2((2))
3((3))
0 --> |100| 1
1 --> |600| 3
1 --> |100| 2
2 --> |100| 0
2 --> |200| 3import heapq
from collections import defaultdict
from typing import List
# Bellman-Ford
def findCheapestPriceBF(
n: int, flights: List[List[int]], src: int, dst: int, k: int
) -> int:
prices = [float("inf") for _ in range(n)]
prices[src] = 0
for _ in range(k + 1):
temp = prices[:]
for u, v, w in flights:
temp[v] = min(temp[v], prices[u] + w)
prices = temp
return prices[dst] if prices[dst] != float("inf") else -1
# Dijkstra
def findCheapestPriceDijkstra(
n: int, flights: List[List[int]], src: int, dst: int, k: int
) -> int:
graph = defaultdict(list)
for u, v, w in flights:
graph[u].append((v, w))
heap = [(0, src, 0)] # (price, city, stops)
visited = defaultdict(int) # {city: stops}
while heap:
price, city, stops = heapq.heappop(heap)
if city == dst:
return price
if stops > k:
continue
if city in visited and visited[city] <= stops:
continue
visited[city] = stops
for neighbor, cost in graph[city]:
heapq.heappush(heap, (price + cost, neighbor, stops + 1))
return -1
# |------------|------------------|---------|
# | Approach | Time | Space |
# |------------|------------------|---------|
# |Bellman-Ford| O(k * E) | O(n) |
# | Dijkstra | O(E * log(V)) | O(n) |
# |------------|------------------|---------|
n = 4
flights = [[0, 1, 100], [1, 2, 100], [2, 0, 100], [1, 3, 600], [2, 3, 200]]
src = 0
dst = 3
k = 1
print(findCheapestPriceBF(n, flights, src, dst, k)) # 700
print(findCheapestPriceDijkstra(n, flights, src, dst, k)) # 700
2699. Modify Graph Edge Weights¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: graph, heap priority queue, shortest path
1810. Minimum Path Cost in a Hidden Grid¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: depth first search, breadth first search, graph, heap priority queue, interactive
2093. Minimum Cost to Reach City With Discounts¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: graph, heap priority queue, shortest path
2473. Minimum Cost to Buy Apples¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, shortest path
2714. Find Shortest Path with K Hops¶
-
LeetCode | LeetCode CH (Hard)
-
Tags: graph, heap priority queue, shortest path
2737. Find the Closest Marked Node¶
-
LeetCode | LeetCode CH (Medium)
-
Tags: array, graph, heap priority queue, shortest path