Binary Tree Traversal

Table of Contents

• 144. Binary Tree Preorder Traversal (Easy)
• 94. Binary Tree Inorder Traversal (Easy)
• 145. Binary Tree Postorder Traversal (Easy)
• 872. Leaf-Similar Trees (Easy)
• 404. Sum of Left Leaves (Easy)
• 671. Second Minimum Node In a Binary Tree (Easy)
• 1469. Find All The Lonely Nodes (Easy) 👑
• 1214. Two Sum BSTs (Medium) 👑
• 2764. Is Array a Preorder of Some ‌Binary Tree (Medium) 👑

144. Binary Tree Preorder Traversal

• LeetCode | LeetCode CH (Easy)

• Tags: stack, tree, depth first search, binary tree

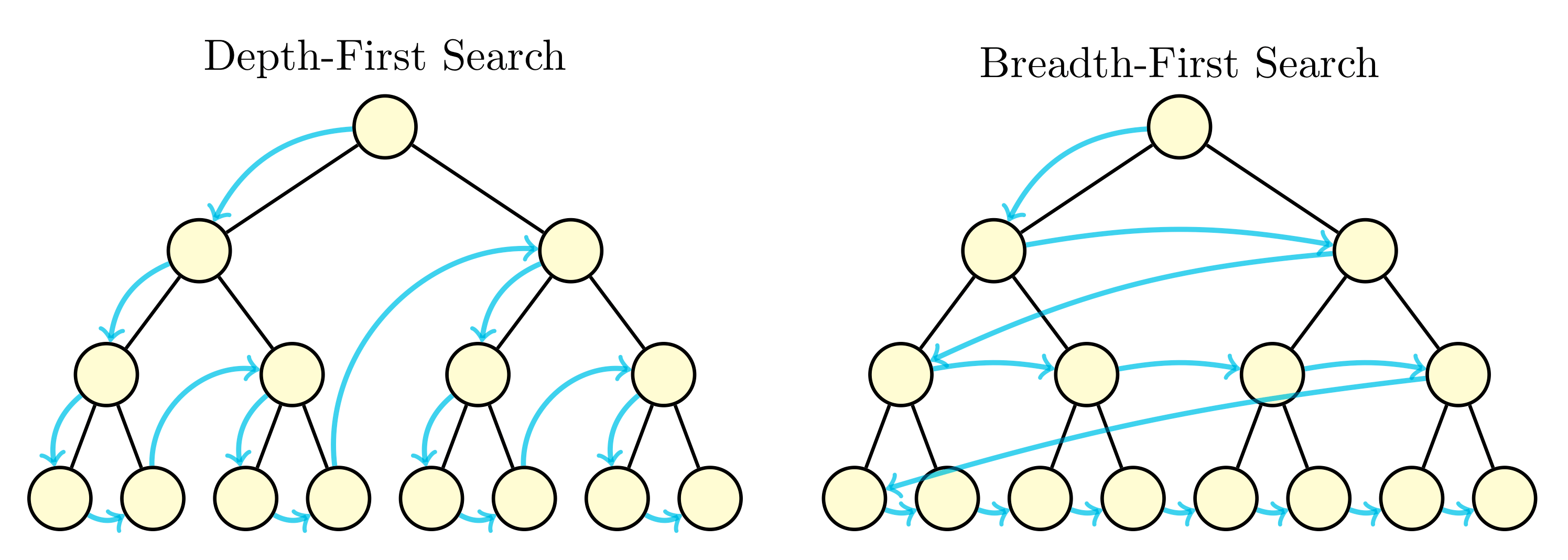
Example 1

graph TD
A(( ))
B(( ))
C(( ))
D(( ))
E(( ))
F(( ))
G(( ))
A --- B
A --- E
B --- C
B --- D
E --- F
E --- G

Pre-order Traversal

graph TD
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
6((6))
0 --- 1
0 --- 4
1 --- 2
1 --- 3
4 --- 5
4 --- 6

In-order Traversal

graph TD
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
6((6))
3 --- 1
3 --- 5
1 --- 0
1 --- 2
5 --- 4
5 --- 6

Post-order Traversal

graph TD
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
6((6))
6 --- 2
6 --- 5
2 --- 0
2 --- 1
5 --- 3
5 --- 4

Level Order Traversal

graph TD
0((0))
1((1))
2((1))
3((2))
4((2))
5((2))
6((2))
0 --- 1
0 --- 2
1 --- 3
1 --- 4
2 --- 5
2 --- 6

Example 2

graph TD
0((0))
1((1))
2((2))
3((3))
4((4))
5((5))
6((6))
0 --- 1
0 --- 2
1 --- 3
1 --- 4
2 --- 5
2 --- 6

Traversal	Order	Method	Result
Preorder	Root, Left, Right	DFS or Stack	[0, 1, 3, 4, 2, 5, 6]
Inorder	Left, Root, Right	DFS or Stack	[3, 1, 4, 0, 5, 2, 6]
Postorder	Left, Right, Root	DFS or Stack	[3, 4, 1, 5, 6, 2, 0]
Level Order	Level by Level	BFS with Queue	[[0], [1, 2], [3, 4, 5, 6]]

144. Binary Tree Preorder Traversal - Python Solution

from typing import List, Optional

from binarytree import Node as TreeNode
from binarytree import build


# Recursive
def preorderTraversalRecursive(root: Optional[TreeNode]) -> List[int]:
    res = []

    def dfs(node):
        if not node:
            return None

        res.append(node.val)  # <--
        dfs(node.left)
        dfs(node.right)

    dfs(root)

    return res


# Iterative
def preorderTraversalIterative(root: Optional[TreeNode]) -> List[int]:
    if not root:
        return []

    stack = [root]
    res = []

    while stack:
        node = stack.pop()
        res.append(node.val)

        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)

    return res


tree = build([0, 1, 2, 3, 4, 5, 6])
print(tree)
#     __0__
#    /     \
#   1       2
#  / \     / \
# 3   4   5   6
print(preorderTraversalRecursive(tree))  # [0, 1, 3, 4, 2, 5, 6]
print(preorderTraversalIterative(tree))  # [0, 1, 3, 4, 2, 5, 6]

94. Binary Tree Inorder Traversal

• LeetCode | LeetCode CH (Easy)

• Tags: stack, tree, depth first search, binary tree

94. Binary Tree Inorder Traversal - Python Solution

from typing import List, Optional

from binarytree import Node as TreeNode
from binarytree import build


# Recursive
def inorderTraversalRecursive(root: TreeNode) -> List[int]:
    res = []

    def dfs(node):
        if not node:
            return

        dfs(node.left)
        res.append(node.val)  # <--
        dfs(node.right)

    dfs(root)

    return res


# Iterative
def inorderTraversalIterative(root: Optional[TreeNode]) -> List[int]:
    if not root:
        return []

    stack = []
    res = []
    cur = root

    while cur or stack:
        if cur:
            stack.append(cur)
            cur = cur.left
        else:
            cur = stack.pop()
            res.append(cur.val)
            cur = cur.right

    return res


tree = build([0, 1, 2, 3, 4, 5, 6])
print(tree)
#     __0__
#    /     \
#   1       2
#  / \     / \
# 3   4   5   6
print(inorderTraversalRecursive(tree))  # [3, 1, 4, 0, 5, 2, 6]
print(inorderTraversalIterative(tree))  # [3, 1, 4, 0, 5, 2, 6]

145. Binary Tree Postorder Traversal

• LeetCode | LeetCode CH (Easy)

• Tags: stack, tree, depth first search, binary tree

145. Binary Tree Postorder Traversal - Python Solution

from typing import List, Optional

from binarytree import Node as TreeNode
from binarytree import build


# Recursive
def postorderTraversalRecursive(root: Optional[TreeNode]) -> List[int]:
    res = []

    def dfs(node):
        if not node:
            return

        dfs(node.left)
        dfs(node.right)
        res.append(node.val)  # <--

    dfs(root)

    return res


# Iterative
def postorderTraversalIterative(root: Optional[TreeNode]) -> List[int]:
    if not root:
        return []

    res = []
    stack = [root]

    while stack:
        node = stack.pop()
        res.append(node.val)

        if node.left:
            stack.append(node.left)
        if node.right:
            stack.append(node.right)

    return res[::-1]


tree = build([0, 1, 2, 3, 4, 5, 6])
print(tree)
#     __0__
#    /     \
#   1       2
#  / \     / \
# 3   4   5   6
print(postorderTraversalRecursive(tree))  # [3, 4, 1, 5, 6, 2, 0]
print(postorderTraversalIterative(tree))  # [3, 4, 1, 5, 6, 2, 0]

872. Leaf-Similar Trees

• LeetCode | LeetCode CH (Easy)

• Tags: tree, depth first search, binary tree

872. Leaf-Similar Trees - Python Solution

from typing import Optional

from binarytree import Node as TreeNode
from binarytree import build


# Tree
def leafSimilar(root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool:

    def dfs(node, leaf):
        if not node:
            return
        if not node.left and not node.right:
            leaf.append(node.val)
        dfs(node.left, leaf)
        dfs(node.right, leaf)

    leaf1, leaf2 = [], []
    dfs(root1, leaf1)
    dfs(root2, leaf2)

    return leaf1 == leaf2


root1 = [3, 5, 1, 6, 2, 9, 8, None, None, 7, 4]
root2 = [3, 5, 1, 6, 7, 4, 2, None, None, None, None, None, None, 9, 8]
root1 = build(root1)

root2 = build(root2)
print(root1)
#     ______3__
#    /         \
#   5__         1
#  /   \       / \
# 6     2     9   8
#      / \
#     7   4
print(root2)
#     __3__
#    /     \
#   5       1__
#  / \     /   \
# 6   7   4     2
#              / \
#             9   8
print(leafSimilar(root1, root2))  # True

404. Sum of Left Leaves

• LeetCode | LeetCode CH (Easy)

• Tags: tree, depth first search, breadth first search, binary tree

404. Sum of Left Leaves - Python Solution

from typing import Optional

from binarytree import build


class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


# Iterative
def sumOfLeftLeaves(root: Optional[TreeNode]) -> int:
    if not root:
        return 0

    stack = [root]
    sumLL = 0

    while stack:
        node = stack.pop()

        if node.left and not node.left.left and not node.left.right:
            sumLL += node.left.val

        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)

    return sumLL


# Left Leave None:
#   - node.left is not None
#   - node.left.left is None
#   - node.left.right is None

root = build([3, 9, 20, None, None, 15, 7])
print(root)
#   3___
#  /    \
# 9     _20
#      /   \
#     15    7
print(sumOfLeftLeaves(root))  # 24

671. Second Minimum Node In a Binary Tree

• LeetCode | LeetCode CH (Easy)

• Tags: tree, depth first search, binary tree

1469. Find All The Lonely Nodes

• LeetCode | LeetCode CH (Easy)

• Tags: tree, depth first search, breadth first search, binary tree

1214. Two Sum BSTs

• LeetCode | LeetCode CH (Medium)

• Tags: two pointers, binary search, stack, tree, depth first search, binary search tree, binary tree

2764. Is Array a Preorder of Some ‌Binary Tree

• LeetCode | LeetCode CH (Medium)

• Tags: stack, tree, depth first search, binary tree

Comments